Adorons Jésus-Eucharistie! | Accueil >> Varia >> Livres >> Précis de philosophie
[précédente] [suivante]
Note: Si le grec classique ne s'affiche pas correctement sur votre fureteur Internet, SVP lire Comment peut-on lire/écrire des caractères grecs dans une page HTML?.
§72) Notion. L'induction en général désigne l'activité de notre raison passant des faits d'expérience (ou vérités particulières) à une vérité universelle [§49]. Elle se rattache donc intimement au travail d'abstraction qui, nous l'avons dit [§10 - §12], caractérise notre intelligence et l'oblige à puiser la matière de ses spéculations dans le monde sensible, en y considérant les natures abstraites et universelles. C'est pourquoi l'induction se rencontre en fait à la base de toutes les sciences, générales et particulières, philosophiques, mathématiques et physiques. Si sa présence est parfois méconnue, c'est qu'elle prend deux formes, l'une que nous appellerons induction au sens large; l'autre au sens strict.
1. L'induction au sens large est le passage effectué par l'esprit, à partir d'un ou de quelques faits d'expérience, à une notion très générale ou à une vérité immédiatement évidente: ainsi commence la vie raisonnable de tout homme [§583]; ainsi encore s'établissent les premières notions fondamentales et les principes premiers en métaphysique et en mathématique [°117]. Pour acquérir en effet les notions d'être, de cause, de substance; et les premiers principes: «Tout a sa nature déterminée», «Tout ce qui commence a une cause», etc.; notre esprit a besoin du monde sensible; et il passe, d'ailleurs sans effort, du concret à l'abstrait. Il en est de même quand il découvre les premières idées mathématiques, de grandeur, d'unité et de nombre, d'égalité; et qu'il formule les équations les plus évidentes: 1 + 1 = 2; deux quantités égales à une même troisième sont égales entre elles, etc. [°118].
Cette première forme d'induction n'est pas au sens propre un raisonnement: quand l'esprit découvre spontanément et comme d'instinct dans les faits d'expérience ces notions générales et ces grandes vérités, il se contente d'exercer son mode propre d'agir qui est l'abstraction, et il en est encore à ses deux premiers actes: la simple conception d'idées et le jugement. Il découvre ainsi les premières vérités; il n'accomplit pas encore ce qui caractérise un raisonnement: le passage d'une vérité à une autre.
Mais cette activité abstractive demeure le fond essentiel de toute induction, même développée en raisonnement véritable; elle en explique la nature et en justifie la valeur. De plus, lorsqu'il s'agit des premières définitions philosophiques ou mathématiques, il convient de distinguer, comme nous l'avons dit [§28, (c)] les diverses étapes dans la formation des idées. Pour acquérir les concepts communs ou même simplement descriptifs, il suffit d'une induction au sens large vulgaire, celle que tout homme pratique à l'école du bon sens; mais pour s'élever au concept essentiel et complet, il faut une induction au sens large scientifique [°119] où l'évidence est mise en relief afin de délimiter nettement les notions ou principes découverts. Il peut être utile de présenter ces dernières inductions sous forme de raisonnement pour mieux constater les bases expérimentales des grandes thèses philosophiques [°120].
2. L'induction au sens strict est le raisonnement par lequel, de vérités singulières ou particulières (faits d'expériences) suffisamment énumérées, l'esprit conclut une vérité universelle: une définition ou une loi. Par exemple, après avoir considéré qu'un grand nombre de corps tombent d'eux-mêmes, y compris ceux que les anciens déclaraient légers (comme on le voit en les faisant tomber dans le vide), on conclut: «Tous les corps sont lourds».
§73). L'originalité du raisonnement inductif éclate en le comparant au syllogisme. Celui-ci en effet se met dès l'abord dans l'ordre abstrait; il part de vérités universelles et descend vers des applications moins générales ou même individuelles; d'où l'exemple classique:
Tout homme est raisonnable, Or Pierre est homme, Donc Pierre est raisonnable.
L'induction au contraire a pour point de départ le concret; elle commence par des faits individuels et s'élève vers des vérités universelles et abstraites. On constate par exemple, que cet homme manifeste de la raison dans sa conduite, et cet autre; et cet autre... Donc tout homme est raisonnable. En ces deux raisonnements, le mouvement de l'esprit apparaît en sens inverse.
Cette première différence est incontestable en bon nombre de cas; mais elle reste superficielle; car le syllogisme ne descend qu'exceptionnellement aux applications individuelles [°121]; et souvent la conclusion et les prémisses ont le même degré d'universalité. La différence profonde et essentielle est dans le moyen dont se sert l'esprit dans l'un et l'autre raisonnement pour découvrir une nouvelle vérité.
Dans le syllogisme, ce moyen est un concept exprimé par un terme universel auquel deux autres concepts sont comparés, en sorte que par une troisième proposition l'esprit constate l'identité ou la non-identité du contenu de ces deux concepts. Par exemple, pour prouver que tout homme est libre, on fait appel à une autre idée universelle, qui contient à la fois l'humanité et la liberté: c'est le moyen terme, âme du syllogisme: et l'on dira:
Tout être intelligent est libre; Or tout homme est un être intelligent, Donc tout homme est libre.
Dans l'induction, l'intermédiaire ou le moyen employé par l'esprit pour aboutir à une vérité universelle est la considération des faits où telles natures universelles se réalisent concrètement. Pour établir, par exemple, que tout homme est libre, on fera une série de constatations. Tel individu, Pierre, exerce des activités libres; et Jean de même; et Paul, etc.; et par là, on voit avec une évidence immédiate d'ordre expérimental que la nature universelle de liberté, d'«être libre», se réalise en ces divers individus. Puis on reprendra ces mêmes individus: Pierre, Jean, Paul, etc. et en les considérant précisément comme exerçant leur activité libre, on constatera qu'ils réalisent aussi la nature universelle d'homme, au moins d'homme adulte et normal. Cette double série d'identité permet de conclure: «Tout homme (adulte et normal) est libre».
Ainsi, tandis que l'âme du syllogisme est le moyen terme, l'induction n'a pas de moyen terme; ce qui en tient lieu, c'est l'énumération des faits, c'est-à-dire des parties subjectives où se réalisent deux natures universelles. Le raisonnement est valable, lorsque l'énumération est suffisante pour que l'esprit constate l'identité entre les sujets individuels et les deux natures qu'il s'agit d'identifier dans la conclusion [°122]. On peut mettre en évidence ce mécanisme logique en proposant l'induction comme suit:
Pierre, Jacques, Jean, Paul, etc. font des actes libres; Or la nature universelle qui, en fonction de la liberté, se réalise en Pierre, Jacques, Jean, Paul, etc. est l'homme (adulte et normal); Donc tout homme est libre.
On le voit, tandis que dans le syllogisme, l'esprit se meut dans le même plan qui est celui des natures universelles et abstraites. Dans l'induction au contraire, l'esprit se meut toujours d'un plan à un autre, des vérités d'expérience qui sont l'objet direct des sensations, aux vérités universelles directement intelligibles. Ce sont donc deux façons de raisonner pleinement irréductibles qui suivent leurs lois propres; et si l'on voulait traiter l'induction comme une espèce de syllogisme, elle pécherait inévitablement contre la 7e règle: la conclusion (universelle) serait toujours plus large que les prémisses [°123]. Mais cette opération reste pleinement valable et légitime, parce qu'elle est l'exercice de l'activité abstractive qui caractérise notre esprit.
Ce travail d'abstraction comporte diverses étapes [§11 et §566]. Après avoir tiré des sujets individuels un certain nombre de natures universelles, d'extension restreinte, on peut de celles-ci abstraire des natures plus générales; et cette seconde étape ascensionnelle garde tous les caractères d'une induction. On fera par exemple, cette induction:
L'or est bon conducteur de l'électricité; et le fer; et l'argent; et le zinc, et le cuivre de même, etc. Or la nature universelle que, par rapport à ce rôle de conduire l'électricité, représentent l'or, le fer, l'argent, le zinc, le cuivre, etc., c'est le métal. Donc tout métal est bon conducteur de l'électricité.
La majeure est ici constituée par une série de propositions universelles obtenues par inductions préalables; mais on les considère seulement comme exprimant une partie de la vérité plus générale évoquée dans la mineure: l'or, le fer, etc., cela veut dire: «quelque métal». Le mouvement inductif va donc en ce cas de vérités particulières à la vérité universelle qui y est contenue, comme le dit la définition. D'ailleurs, dans la logique du mouvement inductif, ces vérités particulières ne sont qu'un résumé d'expérience, en sorte que toute induction, directement ou indirectement, part toujours de faits d'expérience pour s'élever aux natures abstraites et aux vérités universelles. On peut même réaliser ce mouvement inductif en sens inverse, pour appliquer au cas concret les vérités universelles. Si l'on sait par exemple, que tout métal conduit bien l'électricité, en considérant que tel corps, comme ce fil de cuivre, est un sujet où se réalise la nature universelle de métal, on en conclura par induction descendante que ce fil de cuivre conduit bien l'électricité. Mais comme cette application se fait aussi et plus naturellement par un syllogisme, il vaut mieux réserver le nom d'induction au mouvement d'ascension de l'esprit vers les vérités universelles.
Notons enfin que la manière habituelle de présenter l'induction est beaucoup plus simple. Non seulement il n'y a jamais de moyen terme, mais généralement la mineure est sous-entendue. Après avoir énuméré les faits d'expérience, on énonce aussitôt la conclusion; on dira par exemple: «Cet homme est doué de liberté; et cet autre; et cet autre... Donc tout homme est libre». Ce que la mineure exprimée met en lumière, en effet, ce n'est pas un terme nouveau, ou une vérité spéciale qui entrerait comme élément dans l'induction. Ce que la mineure met en lumière, c'est l'acte de l'esprit qui voit une nature universelle dans les sujets concrets dont vient de parler la majeure, et qui voit cette nature en laissant de côté les caractères individuels de façon à retrouver, dans la multiplicité variable des faits d'expérience, le type, immuable et un, qui s'y réalise. Par exemple, c'est l'acte de l'esprit qui voit dans Pierre, Paul, Jean, etc. (agissant librement) l'unique nature humaine, source immuable de l'activité libre de tout individu humain. En d'autres termes, cette mineure exprime la fonction abstractive qui est «l'âme» de l'induction; et en réalité cette fonction n'a pas à être exprimée, mais à être exercée.
On peut cependant pour mettre en forme l'induction, présenter la mineure comme un principe d'interprétation, presque indispensable, à cause des diverses manifestations de ce raisonnement, comme nous allons le montrer.
§74) Division de l'induction. L'induction au sens propre peut être d'abord complète ou incomplète.
L'induction complète est celle dont la conclusion affirme d'une nature universelle une propriété vérifiée de tous les inférieurs de cette nature; par exemple, ayant constaté que l'or, l'argent et tous les autres métaux sans exception sont bons conducteurs de l'électricité, on conclura: «Donc tout métal est bon conducteur de l'électricité».
L'induction incomplète est celle où la propriété affirmée d'une nature universelle n'a été vérifiée que pour un certain nombre d'inférieurs; par exemple, après avoir constaté que quelques hommes en France, puis en Belgique, en Angleterre, en Amérique, etc. sont doués de liberté, on conclut: «Donc tout homme est doué de liberté».
Mais cette dernière peut être suffisante ou insuffisante.
L'induction incomplète suffisante est celle qui fait apparaître clairement un lien nécessaire entre la nature universelle et la propriété (ou prédicat) qu'on lui attribue dans la conclusion.
L'induction sera insuffisante si elle ne fait pas apparaître clairement le lien nécessaire entre le sujet universel et le prédicat de la conclusion. Il y a d'ailleurs de nombreuses nuances en cette clarté et avant d'atteindre la pleine évidence qui donne l'infaillible vérité [§889] on obtient souvent une réelle vraisemblance et une conclusion de plus en plus probable. Par exemple, lorsque Pasteur cherchait à résoudre par induction le problème: «Tout organisme vivant vient-il d'un germe vivant?» les premières expériences, sans être encore décisives, inclinaient son esprit vers l'affirmative; mais ce n'était qu'une induction insuffisante; lorsqu'il eu réfuté toutes les objections possibles, le lien nécessaire entre la nature de l'organisme vivant et la propriété de venir d'un germe apparut clairement: l'induction fut suffisante, mais elle resta incomplète, car Pasteur n'avait pas épuisé tous les cas possibles de génération; leur nombre est du reste inépuisable, puisqu'il est indéfini, embrassant le futur et le passé, comme le présent.
C'est pourquoi la véritable induction scientifique est l'induction incomplète suffisante [°124]. On ne peut en effet réaliser l'énumération complète qu'en deux cas: D'abord, en commençant l'induction au second degré comme dans l'exemple des métaux bons conducteurs de l'électricité; car le nombre de ces groupements n'est pas inépuisable et la majeure inductive peut en fournir la liste complète [°125]; mais c'est là une forme dérivée qui suppose pour chaque vérité particulière une induction fondée sur les faits d'expérience concrets où s'alimente toujours le progrès scientifique et celle-ci est inévitablement incomplète.
On peut cependant parfois, même en commençant par des faits individuels, réaliser une énumération complète; par exemple, Pierre, Jean, Jacques, André, Philippe, Thomas, Simon, Jude, Barthélemy, Mathieu, Jacques le mineur, et Judas étaient présents à la dernière cène. Or ces douze sont tous les apôtres. Donc tous les apôtres étaient présents à la dernière cène. Mais dans ce cas on ne s'élève plus dans la conclusion à une vérité universelle nouvelle; on passe simplement à une collection d'individus qui n'ajoute rien à l'énumération exposée dans la majeure. Il n'y a donc plus d'acquisition de vérité nouvelle ni de raisonnement au sens propre. Le seul moyen de sauvegarder celui-ci est de tirer des faits par abstraction, une vérité vraiment universelle; alors cette conclusion, quoique très légitime, débordera de toute part les expériences invoquées pour l'établir: ce sera l'induction incomplète suffisante.
§75). Cette induction scientifique est d'usage universel, aussi bien dans les sciences philosophiques que dans les sciences positives (dites expérimentales); le mécanisme en est le même et l'efficacité identique; mais la direction en est diverse. C'est pourquoi nous en distinguerons deux formes types: l'une établissant les définitions, l'autre les lois.
a) L'induction scientifique qui conduit aux définitions montre le lien nécessaire entre une nature universelle (prise comme réalité substantielle ou accidentelle) et les notes ou les propriétés qui la constituent essentiellement. Quand elle vise les définitions réelles et essentielles [§33], elle répond au problème propre des sciences philosophiques, qui est le problème des natures [§113]; et s'il s'agit des définitions les plus générales, elle ne se distingue guère de l'induction au sens large; mais pour les définitions plus spéciales, par exemple, celles du mouvement [§253] ou de la liberté [§796], elle est un vrai raisonnement.
Elle peut aussi se rencontrer en sciences positives pour établir des définitions descriptives et des classifications. En ce dernier cas surtout, elle prend la forme d'un vrai raisonnement, usant des méthodes expérimentales; souvent au contraire la définition descriptive d'un phénomène, bien que présentée sous forme universelle, relève d'une simple abstraction sans raisonnement; on se contente de décrire exactement les procédés employés et les instruments de mesure utilisés; seulement, lorsqu'en sciences physico-mathématiques on définit ainsi un phénomène techniquement élaboré, on présuppose, comme nous le dirons [§336-§341] plusieurs lois démontrées et donc, plusieurs inductions préalables.
C'est encore une induction du même genre qui intervient pour prouver les lois appelées descriptives [§151] qui ne sont pas de vraies explications mais servent seulement, comme les définitions, à caractériser un phénomène. Nous avons alors une forme mixte qu'on peut aussi rattacher à la forme suivante.
b) L'induction scientifique qui mène aux lois montre en général le lien nécessaire entre un antécédent et un conséquent. Cet antécédent pourra être une nature universelle (prise comme sujet d'action) et le conséquent une manière déterminée d'agir ou de se comporter; par exemple, après avoir expérimenté sur divers corps avec les instruments requis pour mesurer la chute des corps, on conclura que: «Tout corps tombe dans le vide selon la formule d'accélération e = 1/2 gt2», les corps qui s'attirent étant considérés comme sujets substantiels. L'antécédent et le conséquent peuvent être aussi, dans les phases plus évoluées de la science physico-mathématique [°126], de purs phénomènes techniquement élaborés, constitués par un groupe de mesures prises en fonction d'instruments particuliers; par exemple, dans la loi indiquant le rapport entre la force d'un courant électrique et la chaleur qui s'en dégage, où l'électricité et la chaleur sont définies par les mesures trouvées au galvanomètre et au thermomètre. Cette forme répond donc directement au point de vue des sciences positives qui étudient uniquement le lien nécessaire entre deux phénomènes [§114]. Sans doute le phénomène n'existe pas seul; il suppose une substance où il réside et il a lui-même une nature définissable; mais cette définition ontologique du phénomène et du sujet où il subsiste reste directement hors de cause. Il s'agit uniquement d'établir un lien nécessaire entre l'antécédent et le conséquent considérés comme «apparences», indépendamment des réalités sous-jacentes; ainsi établit-on l'équivalence des deux énergies, celle de l'électricité et celle de la chaleur émise, sans rien savoir de la nature ni de l'électricité ni de la chaleur; ou bien on démontre la loi de la réfraction du rayon lumineux traversant l'eau, sans rien connaître de la nature, ni de l'eau ni de la lumière.
Cette indépendance a d'ailleurs des degrés; et dans certaines formes d'inductions, en chimie par exemple, et surtout en psychologie expérimentale, l'étude des lois régissant les phénomènes commence à dévoiler la nature des substances qui en sont la source. Mais la direction de l'esprit est assez divergente pour qu'il soit utile de distinguer deux formes d'induction: l'une conduisant aux définitions et utilisée surtout en philosophie; l'autre conduisant aux lois et employée principalement en sciences positives modernes.
§76) Principe suprême de l'induction. L'induction étant un raisonnement irréductible au syllogisme, se fonde sur un principe suprême très différent, qu'on peut formuler ainsi: «Ce qui est vrai des parties subjectives suffisamment énumérées, est vrai également du tout universel ou de la nature que ces sujets réalisent».
Rien de plus évident que ce principe, puisque par définition, l'énumération des parties subjectives, c'est-à-dire des faits d'expérience, est suffisante lorsqu'il apparaît clairement que ces sujets par rapport à la propriété considérée, ne sont que des réalisations de telle nature universelle; cette nature en effet prise comme telle est invariable, quels que soient les inférieurs où elle se réalise [°127]; par exemple; la nature humaine est toujours la même, qu'elle se trouve en Pierre ou en Jean, ou en Paul, etc.; et si, vraiment, en quelques individus elle a telle propriété, par exemple d'être principe d'activité libre, elle gardera cette même propriété dans tous les individus sans exception.
Ce principe pourtant régit d'une façon plus directe et plus simple les inductions qui conduisent aux définitions; car l'esprit y considère franchement la nature dont il cherche à préciser les notes, comme un tout logique dont les faits d'expérience ne sont que des réalisations. Au contraire, dans l'induction conduisant aux lois, cette nature reste à l'arrière plan comme un objet de pensée dont on fait abstraction, pour ne considérer que les propriétés ou phénomènes dans leurs rapports mutuels. C'est pourquoi le principe suprême ne s'y applique qu'indirectement, par l'intermédiaire du principe de causalité mutuelle, lui-même fondé sur le principe du déterminisme de la nature [°128] que l'on formule:
«Les mêmes causes physiques, dans les mêmes circonstances produisent toujours les mêmes effets».
Mais il s'agit toujours de découvrir un lien nécessaire, soit entre une nature et ses propriétés, soit entre deux phénomènes soumis au déterminisme.
§77) Règles de l'induction. Toute la difficulté consiste à déterminer quand l'énumération est suffisante pour faire apparaître ce lien nécessaire. Les conditions requises varient avec les diverses sciences positives, et on les exposera en méthodologie spéciale; nous formulerons seulement ici deux règles générales qui suffiront le plus souvent pour les inductions conduisant aux définitions.
1) Règle de l'énumération. Les faits énumérés doivent être exactement observés et suffisamment variés pour que toute hypothèse imaginable, autre que la définition ou la loi supposée vraie soit éliminée. Par exemple, si l'on définit la vie par le mouvement immanent, il faut qu'aucun fait incontestable de vie ne se rencontre sans ce mouvement immanent.
2) Règle du Principe d'interprétation. Il faut préciser nettement la nature universelle en fonction de laquelle on rassemble les faits d'expérience; car les mêmes faits peuvent s'interpréter de plusieurs manières d'ailleurs également légitimes. Ainsi, l'assimilation des aliments par le vivant peut servir, soit à définir la vie par le mouvement immanent, soit à établir la loi physique d'action et réaction, soit aussi à découvrir les principes constitutifs requis dans l'aliment (matière et forme) pour subir une transformation si profonde [°129]. Cette multiplicité de directions possibles oblige l'esprit à choisir son orientation; il le fait en formulant une hypothèse, ou plus généralement un principe d'interprétation à la lumière duquel il voit dans l'expérience une vérité universelle de tel ordre déterminé. Par exemple, après avoir énuméré les faits d'assimilation vitale, le principe du déterminisme de la nature y fera constater la loi de la conservation de l'énergie; le principe de raison suffisante y fera voir la définition de la vie par l'immanence. Ainsi les premiers principes qui orientent le travail inductif sont des vérités immédiatement évidentes qui s'imposent à tout observateur de bon sens; tels sont en particulier les deux principes suprêmes mentionnés plus haut. Mais ces principes sont encore trop généraux, et il faut à l'esprit une direction plus précise: celle-ci est obtenue dans les sciences positives en formulant une hypothèse, comme nous le montrerons [§121]. Dans les sciences philosophiques, on suit la même méthode en formulant une thèse qui n'est d'abord qu'une proposition à démontrer (hypothèse). Mais de plus, pour éclairer le regard de l'esprit cherchant à lire dans les faits la définition ou la thèse universelle à démontrer, on fait appel à un principe préalablement établi et qui se rattache au principe de raison suffisante comme une application spéciale. Par exemple, après avoir rassemblé les faits d'activité immanente, on en conclura la définition de la vie à la lumière de ce principe: «Une nature se définit par ses propriétés (ou perfections) nécessaires et exclusives», car l'unique façon d'expliquer ces propriétés (d'en donner la raison suffisante) est de poser une nature spécifiquement distincte qui en soit la source [°130].
Il suit de là, que la façon la plus simple de mettre en forme une induction est d'énoncer dans la majeure une série de faits d'expérience bien observés et suffisamment variés; et dans la mineure, le principe d'interprétation à la lumière duquel apparaîtra dans les faits la vérité universelle qu'il s'agit de démontrer.
§78) Raisonnement par analogie. Le raisonnement par ressemblance ou par analogie [°131], est celui qui, de certaines ressemblances constatées entre deux sujets, conclut à l'existence d'autres ressemblances non constatées. Par exemple, James Watson voit des crystallographies aux rayons-X de molécules hélicales; or l'ADN produit exactement le même genre de crystallographies, comme le montre le travail de Rosalind Franklin; donc il en conclut que l'ADN pourrait avoir une structure hélicale.
Ce raisonnement se rattache à l'induction, bien qu'il passe, semble-t-il, directement d'un cas particulier à un autre cas particulier; mais il le fait à la lumière d'un principe rationnel et non par simple association d'image [°132]; et ce principe n'est autre que celui du déterminisme de la nature; car si une même cause produit toujours les mêmes effets, à supposer que dans un premier cas les diverses propriétés observées forment un groupe indissoluble ayant un lien nécessaire avec telle nature, partout où l'on retrouvera une de ces propriétés, on retrouvera aussi les autres. Nous avons donc bien une induction où les faits sont interprétés à la lumière d'un principe. Il faut noter seulement que si l'esprit veut accomplir normalement son progrès vers le vrai, il doit expliciter sa démarche, s'élever d'abord à une loi générale (dans l'exemple donné ce serait: «Quiconque a tel type de crystallographie aux rayons X, a telle structure moléculaire»), puis dans la conclusion redescendre par syllogisme ou application inductive à un autre cas particulier. Le plus souvent cette loi restée sous-entendue n'est nullement certaine et nous n'avons qu'une induction incomplète insuffisante dont la conclusion reste probable ou hypothétique. Le rôle de ce raisonnement est d'amorcer la preuve plutôt que de prouver.
Cependant l'analogie est un procédé très fréquent, non seulement dans la vie courante, mais dans les sciences où elle suggère des hypothèses fécondes [§121]. On en distingue plusieurs formes.
a) Au point de vue de la matière: 1) La ressemblance des moyens suggère celle des fins; ainsi les mêmes organes doivent avoir les mêmes fonctions: le poisson fait circuler de l'eau sur ses branchies, comme l'homme fait circuler l'air dans ses poumons, donc on peut penser que le poisson respire par ses branchies. - 2) La ressemblance des effets suggère celle des causes, ainsi Franklin en voyant les effets de l'électricité (étincelle, bruit) ressembler à ceux de l'orage, en conclut que la foudre était un phénomène électrique. - 3) La ressemblance des natures suggère celle des propriétés; si telle espèce de champignon est vénéneuse, telle autre qui lui ressemble doit l'être aussi.
b) Au point de vue de la forme, on distingue le raisonnement a pari qui va du même au même: si les roches ici ont connu la même morphogénèse que celles où on a déjà trouvé du minérai de nickel, il y a peut-être un gisement ici; le raisonnement a fortiori, qui va du moins au plus: s'il faut aimer ses compatriotes, à plus forte raison ses parents; - le raisonnement a contrario qui va d'un contraire à l'autre: si l'abus de l'alcool est funeste à la santé, l'abstinence totale doit lui être utile.
L'exemple ou la comparaison se rattache au raisonnement par analogie comme une ébauche au modèle. Il consiste à illustrer une affirmation, une doctrine, une loi physique ou morale par un fait sensible bien connu, qui aide à le comprendre par comparaison. Il ne s'agit donc plus de prouver, mais d'aider l'esprit à saisir une vérité démontrée par ailleurs, en lui fournissant le «schème» sensible dont il a besoin, selon la grande loi psychologique de dépendance empirique [§548], pour comprendre les rapports intelligibles; aussi serait-il injuste d'apprécier la valeur d'une thèse sur les exemples invoqués dans l'exposé [°133]. «Les exemples choisis, dit Maritain [°134] peuvent être faux en eux-mêmes, ils sont bons, s'ils servent à la manifestation d'une vérité». Ainsi en est-il de tant de comparaisons charmantes empruntées par saint François de Sales aux Histoires naturelles des anciens: «Et comme l'arc-en-ciel touchant l'épine aspalathus la rend plus odorante que le lys, aussi la rédemption de Notre-Seigneur touchant nos misères, elle les rend plus utiles et aimables que n'eut jamais été l'innocence originelle» [°135].
b5) Bibliographie générale (Logique matérielle)
§79). On peut comparer notre intelligence à un récipient capable de recevoir les objets connaissables selon la capacité de ses idées, de ses jugements et de ses sciences. Ces objets constituent ainsi la matière dont nos divers actes d'intelligence sont la forme. Et puisque la science est, comme nous l'avons dit [§16], une connaissance évidente et certaine d'un objet nécessaire et immuable, il ne suffit pas pour l'acquérir de diriger notre raison selon les règles de la logique formelle. En effet, du côté de l'objet ou de la matière, d'autres conditions sont requises. Elles sont exposées en logique matérielle.
La logique matérielle est donc l'ensemble des règles qu'il faut suivre pour bien ordonner la matière des actes d'intelligence afin d'obtenir une vue scientifique parfaite des choses.
Comme nous avons trois actes principaux d'intelligence, la simple appréhension [°136], le jugement et le raisonnement, nous devons chercher la meilleure façon d'ordonner la matière de chacun d'eux. Mais le jugement étant le centre où aboutissent les deux autres actes [§16], ne demande pas de règle spéciale; en considérant la matière, soit de nos concepts, soit de nos raisonnements, nous chercherons toujours la manière de les combiner pour aboutir à des jugements doués de vérité scientifique. Par contre, la matière des sciences pose des problèmes nouveaux d'agencement logique; soit pour lier en un tout harmonieux l'ensemble des sciences, soit pour déterminer la façon spéciale de raisonner en chacune d'elle; c'est à ces dernières considérations que revient spécialement le titre de «méthodologie».
La logique matérielle se divise donc en trois chapitres:
Chapitre 1. - La matière des concepts
Chapitre 2. - La matière des raisonnements
Chapitre 3. - La matière des sciences ou Méthodologie
§80). Nos concepts abstraits ont pour matière ou contenu, comme nous l'avons dit [§12], les essences douées d'éternité, d'immutabilité, de nécessité et d'universalité, d'où leur nom d'universaux. Or la logique matérielle établit une classification de ces essences, d'abord selon la manière dont elles se réfèrent à leurs inférieurs, et nous avons les univoques et les analogues; puis d'après la manière dont on les attribue à un sujet, et ce sont les cinq prédicables; enfin, elle distribue l'ensemble des univoques en divers groupes homogènes: ce sont les dix prédicaments. De là, trois paragraphes en ce chapitre.
1. - Analogie et univocité
2. - Les prédicables
3. - Les prédicaments
b6) Bibliographie spéciale (analogie et univocité)
§81) Notion générale. La propriété logique d'univocité et certaines formes d'analogie conviennent également aux concepts et aux termes qui en sont les signes sensibles; mais il y a des espèces d'analogie, voisines de l'équivocité, qui ne conviennent qu'aux termes. C'est pourquoi nous définirons d'abord ce qu'est le terme univoque, équivoque et analogue [°137].
1) Le terme univoque est celui qui désigne une nature dont le degré de perfection reste pleinement le même dans tous les inférieurs [°138] où elle se réalise («Ratio simpliciter una vel eadem»). Ainsi le mot «Homme» désigne la même nature humaine également réalisée en Pierre, Jean, Suzanne, Judith, etc.
2) Le terme équivoque est celui qui signifie plusieurs natures qui n'ont pas de rapports entre elles («Rationes simpliciter diversae»); ainsi le terme «Chien» désigne à la fois un animal et une partie d'un fusil; le mot latin gallus se traduit par gaulois ou coq. Et comme le terme désigne les natures par l'intermédiaire des concepts, il est clair qu'il faut autant de concepts que de natures signifiées, non sans confusion, par le même terme équivoque; tandis qu'au terme univoque, correspond toujours un seul et même concept signifiant une même nature. Cependant la matière de nos sciences ne se prête pas toujours à cette dernière précision, si désirable soit-elle. On recourt alors à l'analogie.
3) Le terme analogue est celui qui désigne un mode d'être dont le degré de perfection varie en ses divers inférieurs, mais de telle sorte que ceux-ci restent en rapport mutuel; par exemple, le terme vie désignant à la fois l'assimilation nutritive d'une plante et l'activité psychologique de la pensée: le degré d'être dans la vie matérielle ou spirituelle est radicalement divers («Ratio simpliciter diversa»); il reste pourtant un certain rapport entre l'activité immanente de la cellule et celle de l'esprit («Ratio secundum quid eadem vel una»).
§82) Division de l'analogie. Pour préciser cette idée générale d'analogie, les auteurs ont proposé diverses classifications. Voici, semble-t-il, la plus claire, inspirée de la doctrine thomiste.
Il y a d'abord deux grandes formes d'analogie: celle d'attribution et celle de proportionnalité.
1) L'analogie d'attribution est celle où la nature signifiée convient en ordre principal à un des inférieurs (le suprême analogué), et est attribuée aux autres en raison d'un lien de causalité. Par exemple, la santé dite d'un homme sain, d'un aliment sain, d'une couleur saine, convient principalement à l'homme, puis à l'aliment parce qu'il est cause efficiente de santé, à la couleur comme cause significative, etc. On voit que le lien causal peut être très large pour motiver cette analogie.
2) L'analogie de proportionnalité est celle où les diverses natures signifiées sont rassemblées sous le même terme par une ressemblance de proportions ou de rapports qualitatifs inclus dans cette nature; par exemple, en considérant la vie en soi, ce que la cellule réalise dans l'ordre matériel, l'intelligence le fait dans l'ordre spirituel: de part et d'autre, il y a assimilation vitale, activité immanente. L'expression «proportionnalité» fait allusion aux rapports mathématiques entre divers nombres; cette comparaison est éclairante; mais il s'agit ici de rapports qualitatifs, c'est-à-dire entre divers degrés de perfection, et non de quantité, ce qui demande une manière de penser beaucoup plus souple et nuancée [°139].
Pour mieux comprendre cette analogie, il faut en distinguer deux formes.
a) L'analogie de proportionnalité propre est celle où le mode d'être signifié se réalise dans tous les inférieurs selon une même définition; ainsi la vie, définie comme activité immanente, se retrouve bien dans la cellule vivante, dans l'intelligence créée de l'homme, ou dans la pensée infinie de Dieu.
b) L'analogie de proportionnalité métaphorique (ou impropre) est celle où le mode d'être signifié ne convient au sens propre (selon sa définition) qu'à une seule catégorie d'inférieurs, et aux autres, suivant quelque similitude accidentelle seulement. Ainsi le «pied» se dit analogiquement de l'homme et de la montagne, car il y a ressemblance de fonction entre la base de l'un et de l'autre; mais au sens propre le pied comme moyen de locomotion ne convient qu'à l'homme, et pour l'attribuer [°140] à la montagne, il faut changer sa définition. Bref, en ce dernier cas, on parle par métaphore et on se rapproche de l'équivoque: le même terme désigne alors deux concepts qui expriment chacun une nature différente.
Au contraire, dans l'analogie de proportionnalité propre, le même terme correspond à un seul concept, comme dans l'univoque; on a dans la pensée une même nature qui pourra servir de point de comparaison (de moyen terme) pour découvrir une nouvelle vérité scientifique par raisonnement. Mais cette unité du concept objectif analogue pose un problème: Comment est-elle conciliable avec la diversité des degrés de perfection dans les inférieurs, par où l'analogue se distingue de l'univoque?
La conciliation serait impossible en effet, si l'objet de pensée représenté par le concept était une nature absolue, exigeant partout le même degré d'être, comme c'est le cas de l'univoque; l'animalité, par exemple, dans un chien comme dans un homme, a le même degré de perfection, celui de la connaissance sensible. Mais dans l'analogue, l'objet pensé est une nature relative, capable de rester la même et de garder son unité, tout en s'identifiant à des degrés de perfection totalement différents. C'est ce qu'on éclaire par comparaison avec certaines propriétés des nombres; le double, par exemple, désigne beaucoup de nombres très différents, non point tous, mais tous les nombres pairs; 10 est un double (à savoir de 5), et 36 est un double (à savoir de 18): le double est une notion relative, une similitude de proportions quantitatives. Or, par le concept analogue, on pense à quelque chose de semblable dans l'ordre qualitatif; la vie par exemple, ne désigne pas une nature absolue, mais une similitude de rapports entre l'assimilation matérielle de l'aliment par la cellule, et l'assimilation psychologique de l'objet connu par l'esprit. En signifiant ainsi une propriété relative, le concept analogue peut garder une véritable unité, une même définition (du moins au sens large) [°141] tout en exprimant à la fois des degrés divers de perfection, comme le corps et l'esprit, le fini et l'infini.
3) On distingue aussi l'analogie d'attribution au sens strict et au sens large.
La première, (au sens strict), est celle où la nature signifiée ne convient au sens propre (selon sa définition) qu'au suprême analogué; ainsi la santé ne peut réaliser sa définition que dans le vivant, comme l'homme, non dans la couleur ou l'aliment.
La deuxième, (au sens large) est celle où le mode d'être attribué se rencontre en tous les inférieurs avec sa définition, quoique il convienne d'abord suréminemment au suprême analogué. Mais dans ce cas, l'attribution contient virtuellement une analogie de proportionnalité qui seule explique, comme nous l'avons dit, l'identité à divers degrés d'un mode d'être relatif. Ainsi la vie attribuée à Dieu et aux créatures vivantes peut être classée dans l'analogie d'attribution, parce que la vie divine est la cause dont participe toute vie créée; mais il y a en même temps proportionnalité, en sorte que non seulement Dieu, mais ces créatures sont formellement vivantes.
Concluons que seule, avec l'univocité, l'analogie de proportionnalité propre fournit des concepts utilisables pour raisonner juste et construire les sciences.
§83) Rapport avec l'abstraction. Si l'on considère les trois degrés d'abstraction décrits plus haut [§13], il faut dire que les deux premiers fournissent des notions univoques, tandis que les concepts analogues sont le fruit du troisième degré d'abstraction métaphysique. Or l'abstraction métaphysique, en dégageant une perfection de toute matière, lui confère un caractère de plénitude et de pureté qui la fait de droit réalisable à l'infini; mais aussi cette perfection se distingue moins nettement des autres à cause même de son extension très vaste. Au contraire, le concept univoque présente une nature bien délimitée par les notes [°41] matérielles qu'elle conserve encore; mais sa perfection est moins absolue. C'est pourquoi on parlera, d'une part, de perfection pure pour les analogues, et mixte pour les univoques; et d'autre part, d'abstraction parfaite pour ceux-ci, imparfaite pour ceux-là.
La perfection pure est celle qui dans sa définition ne comporte aucune limite: elle ne l'inclut pas de soi, sans cependant l'exclure, comme on le voit par expérience; ainsi la vie sera limitée dans le végétal et infinie en Dieu.
La perfection mixte est celle qui inclut dans sa définition une note de limite; ainsi l'humanité, qui exige le corps.
L'abstraction [§12 et §966] parfaite est celle où l'essence considérée à part est bien délimitée, en sorte que les éléments laissés de côté sont en dehors d'elle et n'y sont éventuellement contenus qu'en puissance. Ainsi la perfection d'animalité contient, en un sens, la rationnalité, puisqu'il est vrai que l'homme est animal; mais de droit, elle lui reste étrangère et peut très bien se réaliser sans elle, par exemple, dans le chien.
L'abstraction imparfaite est celle où la perfection considérée à part contient de droit, en acte, toutes les autres perfections, mais ne les exprime qu'implicitement. L'exemple le plus clair est celui de l'être, la première des idées analogues; car de droit, toute perfection est un mode d'être contenu actuellement dans l'extension du concept d'être; mais au début, l'esprit ne porte explicitement son attention que sur le seul caractère d'être, les autres restant encore ignorés ou implicites; et l'on peut toujours s'efforcer de ne garder devant l'esprit que ce seul caractère, en omettant les autres ou en les laissant implicites. La perfection ainsi obtenue, à cause même de sa généralité et pureté, est apte à se réaliser selon divers degrés, à l'infini et au fini, comme on le voit dans le concept analogue.
Il y a donc toujours correspondance, d'une part, entre concept univoque, perfection mixte et abstraction parfaite; et d'autre part, entre concept analogue (de proportionnalité propre), perfection pure et abstraction imparfaite.
Les perfections pures exprimées par les concepts analogues sont la matière de la métaphysique qui les ordonne selon ses règles propres. Mais les concepts univoques, objets des autres sciences, mathématiques et physiques, donnent lieu aux classifications logiques générales des prédicables et des prédicaments.
§84) Notion. Bien que toute idée abstraite soit universelle, on appelle universel au sens strict, le concept objectif identifiable univoquement à plusieurs inférieurs en nombre indéterminé; ainsi l'animalité s'attribue à tous les hommes, tous les chiens, etc. Or cette attribution peut se faire diversement, et l'analyse découvre cinq manières possibles. Si l'on dit par exemple, Pierre est homme ou animal, ou raisonnable, ces trois qualités appartiennent bien à l'essence de Pierre, mais la première comme désignant cette essence complète, les deux autres comme en signifiant une partie seulement; et l'animalité, la partie inférieure la moins parfaite, commune à d'autres espèces d'être; la rationalité, la partie la plus parfaite qui différentie l'homme des autres animaux. Si nous ajoutons: Pierre est libre; ou Pierre est musicien, ces deux qualités lui conviennent en dehors de son essence humaine, de telle sorte cependant que la première garde un lien nécessaire avec elle, et la seconde au contraire lui reste indifférente.
On appelle prédicable la manière dont la perfection exprimée par un concept univoque peut s'attribuer à un sujet. Les cinq manières analysées sont l'espèce, le genre, la différence spécifique, le propre et l'accident; et ces mots désignent, soit la manière elle-même, soit aussi la nature universelle sous l'angle de telle ou telle façon d'être attribuable à un sujet.
L'espèce est l'universel comme attribuable au titre d'essence complète; ainsi l'humanité est une espèce pour Pierre et Paul.
Le genre est l'universel attribuable au titre d'essence incomplète, commune à plusieurs espèces; ainsi l'animalité est un genre pour l'homme, le chien, l'oiseau, etc.
La différence spécifique est l'universel attribuable au titre de qualité essentielle caractéristique d'une espèce; ainsi la rationalité pour l'homme.
Le propre est l'universel attribuable au titre de détermination (ou qualité) liée nécessairement à une essence (générique ou spécifique), en sorte qu'il lui convient à elle seule, partout et toujours; ainsi la risibilité ou la parole pour l'homme; la quantité pour le corps.
L'accident est l'universel attribuable à un sujet d'une façon contingente; ainsi la qualité de médecin pour l'homme: elle lui est indifférente et peut être absente ou présente.
Quant au sujet lui-même auquel on attribue ces natures, il est en dernière analyse, non plus un universel, mais un individu.
L'individu au point de vue logique est ce qui ne peut convenir et être attribué qu'à un seul. Il est l'inférieur de tous les autres universaux et n'a lui-même aucun inférieur auquel il pourrait être attribué. Aussi ne peut-on s'en former une idée abstraite spéciale; puisqu'il est précisément le réel concret; l'intelligence le connaît par ses autres idées et spécialement par son idée analogue d'être [°142]; et l'individualité est une propriété qui ne convient qu'analogiquement à tous les individus.
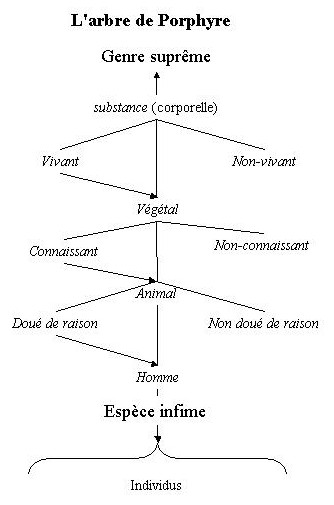
§85) Notion. Les perfections de l'univers corporel qui peuvent ainsi s'attribuer de cinq façons à un sujet sont en nombre considérable et très diverses. Il est possible cependant de les classer en catégories qui faciliteront leur étude. Car d'abord il en est qui ont entre elles d'évidentes affinités, en sorte qu'elles ont les unes par rapport aux autres des relations de genre, d'espèce, de différence spécifique qui permettent de les ordonner en gradation descendante sous forme d'arbre appelé «arbre de Porphyre» [PHDP §122]. Ainsi à partir de la substance corporelle jusqu'à l'homme, on trouve une série liée de perfections: le genre corporel se divise en deux espèces: vivants et non-vivants; le vivant à son tour, en connaissant et non-connaissant; le connaissant en raisonnable et irraisonnable; et chaque branche supérieur peut s'attribuer au tronc inférieur. Dans cette ordonnance, il y a un genre suprême: la substance (corporelle): celui au-dessus duquel il n'en existe pas de plus large en extension; et des espèces infimes, par exemple, l'homme, le cheval, etc., celles qui ne contiennent dans leur extension que des individus de même espèce; entre les deux extrêmes s'échelonnent les genres et les espèces intermédiaires.

Si on prenait les figures géométriques, on les verrait certes irréductibles à l'arbre que nous venons de construire; mais elles s'ordonnent entre elles de même façon, par genre, espèces, différences spécifiques. À côté des figures, les facultés ou puissances opératives; et à côté encore, les vertus et les vices manifestent de semblables affinités; et ces trois enchaînements de perfections constituent les trois branches principales qui se rejoignent dans un tronc commun comme dans un nouveau genre suprême: la qualité. Bref, on constate que toutes les perfections du monde exprimables en concepts univoques, s'ordonnent spontanément sous quelques genres suprêmes; et l'analyse a conduit Aristote à en dénombrer 10: ce sont les dix prédicaments (ou «10 catégories»).
Le prédicament [°143] est donc, au point de vue réel, l'un des genres suprêmes entre lesquels se divisent toutes les perfections du monde physique; - au point de vue logique, l'ordre hiérarchique lui-même des genres, espèces et différences spécifiques qui s'échelonnent sous chacun de ces genres suprêmes.
§86) Les dix prédicaments (ou «catégories», ou «attributions»). Parmi ces perfections exprimées en concepts univoques, on distingue d'abord deux grands groupes: les substances et les accidents.
La substance est l'essence à laquelle il convient d'exister en soi et non dans un autre.
L'accident est l'essence à laquelle il convient d'exister dans un autre comme dans un sujet d'inhésion. Par exemple, l'humanité est une substance; la blancheur et la science sont des accidents. L'existence de la substance est la subsistance: un homme existe réellement en soi et on le rencontre dans la nature. L'existence de l'accident est l'inhérence: une blancheur séparée qui ne serait la blancheur ni d'un homme, ni d'une craie, ni du marbre, etc., n'existe nulle part dans la nature.
Mais, étant donné que notre concept de substance est abstrait, la nature à laquelle on pense, par exemple la nature humaine, se rencontre sous deux modes d'êtres très différents: dans les êtres réels, Pierre, Élisabeth, Paul, etc., où elle est individuelle et multipliée; et aussi dans notre concept abstrait où elle est universelle et unique en son espèce (ou en son genre). On appelle substance première, celle qui existe dans la nature comme individu subsistant; et substance seconde, celle qui est contenue dans le concept abstrait, comme nature universelle.
On peut dire que la substance seconde existe dans les individus comme dans un sujet d'attribution logique: ainsi Pierre, Jean, Paul, etc. sont homme: la substance humaine (substance seconde) leur est évidemment attribuée; mais de ce fait, la substance seconde ne devient pas un accident de la substance première, car elle lui est en réalité pleinement identique [°144] comme essence ou nature. Par exemple, la nature substantielle à laquelle nous pensons en disant: «Pierre est homme» est unique et la même dans l'individu Pierre (substance première) et dans l'idée abstraite d'humanité (substance seconde); tandis que l'accident est une essence distincte, comme l'essence de la blancheur ou de la science, distincte de la nature humaine; et elle existe dans la substance comme dans un sujet d'inhésion et non plus seulement comme dans un sujet d'attribution.
Aristote énumérait neuf prédicaments accidents: les trois principaux sont la quantité, la qualité, la relation.
La quantité est le mode d'être qui donne à la substance corporelle des parties homogènes les unes en dehors des autres; par exemple, la hauteur d'un arbre.
La qualité est l'accident qui affecte la substance par mode de perfection ou d'actualité («per modum formae»), par exemple: la chaleur, la science, etc.
La relation est le mode d'être par lequel on désigne une chose en fonction d'une autre. Comme prédicament, elle n'est pas un simple être de raison, comme les rapports entre concepts, étudiés en logique; mais c'est une réalité de la nature [°145], par exemple: la paternité, la ressemblance entre un homme et son fils.
À la quantité se rattache le lieu et le temps [°146]; à la qualité, l'action et la passion. Il appartient à la Philosophie naturelle d'établir par induction ces diverses définitions et de justifier l'existence réelle de ces modes d'être en tant que distincts.
Notons seulement ici la différence entre accident prédicable et accident prédicament. Le premier désigne une manière d'«être attribué» ou une relation logique entre le prédicat et le sujet dans un jugement; le second désigne une manière spéciale d'«exister» ou la nécessité d'avoir un sujet d'inhésion pour se réaliser dans la nature; mais tous les modes d'êtres accidentels peuvent rentrer dans l'un ou l'autre prédicable: genre; espèce, propre, accident, etc., selon les cas. Ainsi en disant: «Tout homme est libre», la liberté est un propre, non un accident prédicable; mais c'est un accident prédicament. De même en disant: «Tout carré est une figure», la figure comme prédicable, est un genre, comme prédicament, une qualité, c'est-à-dire un accident.
b7) Bibliographie spéciale (la matière des raisonnements)
§87). C'est en comparant entre elles les natures abstraites rangées selon les dix prédicaments et en les unissant selon les lois des cinq prédicables que l'intelligence forme des jugements vrais. Si les jugements sont immédiats, ils ne sont pas encore la science; car pour nous, la connaissance parfaite ou scientifique suppose, à partir des premières intuitions, un effort d'analyse, puis de synthèse, où les propriétés de l'objet étudié sont pleinement expliquées par leurs causes, grâce au raisonnement rigoureux, appelé démonstration.
Cependant, il n'est pas toujours possible de réaliser les strictes exigences de la science. Souvent la raison est en présence de données qui, sans manquer de valeur, n'atteignent pas la nécessité absolue de l'infaillible vérité. On doit alors se contenter d'opinions probables. Parfois même on rencontre des affirmations erronées qui se présentent sous les dehors de la vérité à l'aide de raisonnements captieux: ce sont les sophismes qu'il faut connaître pour s'en préserver.
Ce chapitre doit donc examiner trois questions:
1. - La démonstration
2. - Le raisonnement probable
3. - Les sophismes
§88) Notion et division. En général, on appelle «démonstration» tout raisonnement dont la conclusion est vraie et certaine. La science étant la connaissance parfaite d'un objet [§16] est évidemment le fruit de la démonstration; mais celle-ci a un sens plus large; elle distingue simplement au point de vue de la matière le groupe des raisonnements qui aboutissent pleinement à une vérité, par opposition à ceux qui ne l'atteignent qu'imparfaitement ou conduisent à l'erreur.
Nous ne parlerons ici que de la démonstration au sens propre [°147]: celle où la conclusion est distincte des prémisses et qui, par conséquent, suppose un véritable raisonnement avec passage d'une vérité à une autre.
Elle se présente sous deux formes qu'on peut appeler parfaite et imparfaite.
1) La démonstration parfaite (propter quid) est celle qui explique un effet par sa cause propre et directe; on prouvera par exemple, l'immortalité de l'âme par sa spiritualité, celle-ci étant la raison d'être adéquate de celle-là.
La cause dont il s'agit ici désigne toute raison d'être explicative, soit au sens de cause physique, c'est-à-dire réellement distincte de son effet; soit au sens de cause métaphysique, c'est-à-dire n'ayant à l'égard de son effet qu'une distinction de raison, comme lorsqu'on établit l'attribut divin d'éternité au moyen de l'immutabilité.
Seule cette démonstration répond à l'idéal de la science décrit plus haut [§16 - §17]; c'est pourquoi on l'appelle aussi démonstration au sens strict, et comme le raisonnement capable de mettre en pleine lumière cette cause pleinement explicative est le syllogisme, on peut définir la démonstration au sens strict: «Le syllogisme qui engendre la science» [°148].
2) La démonstration imparfaite (quia) est celle qui établit l'existence de la chose ou d'une propriété sans en donner l'explication; on prouvera, par exemple, que Dieu est éternel parce qu'il a toute perfection.
Elle peut être: a posteriori, si elle établit l'existence d'une cause par ses effets; - a priori, si elle démontre l'effet par sa cause (mais par une cause éloignée); - a simultaneo, si la conclusion est sur le même plan que les prémisses. Cette dernière forme est presque a priori; elle reste imparfaite, parce qu'elle ne fait guère avancer l'esprit [°149].
Toute induction ou preuve a posteriori n'est qu'une démonstration imparfaite; elle ne donne qu'une science en formation ou n'en constitue que l'étape préliminaire où sont établies les définitions.
Toute démonstration parfaite au contraire est a priori; mais elle donne la cause propre, sans se contenter d'une cause éloignée et générale.
3) À un autre point de vue, on distingue la démonstration directe et indirecte. a) La démonstration directe est celle qui établit positivement la conclusion. b) La démonstration indirecte est celle qui établit la conclusion en montrant que sa contradictoire est fausse ou impossible; on l'appelle aussi réduction à l'absurde.
§89) Base de la démonstration et procédés généraux de pensée. Comme nous l'avons dit [§15], notre intelligence acquiert ses premières idées sans raisonnement, par une sorte d'intuition. Si, en effet, on devait tout démontrer, on irait à l'infini; autant dire qu'on n'atteindrait jamais la certitude ni la vérité.
Le jugement immédiat ou proposition connue de soi («propositio per se nota») est celui où le rapport (d'identité ou de non-identité) entre le prédicat et le sujet est affirmé uniquement en raison de ces deux termes, sans l'intermédiaire d'aucun autre («propositio quae caret medio»); par exemple, on affirme sans hésiter: Le tout est plus grand que sa partie.
On distingue le jugement immédiat en soi et pour nous. Il est immédiat en soi dès que le prédicat exprime une note qui appartient à l'essence du sujet, même si nous n'en avons pas l'évidence; il l'est pour nous, si les deux termes nous sont assez connus pour que leur relation nous apparaisse clairement. On peut encore préciser: immédiat pour tous ou pour les sages seulement, suivant que cette connaissance des deux termes exige ou non une étude spéciale du sujet; ainsi l'affirmation «L'être est ce qu'il est» est connue de soi pour tous; mais cette autre «Aucun ange n'est dans un lieu», demande pour être comprise une étude des «formes pures» accessible seulement aux philosophes: elle est immédiate pour le sage seulement.
Tout jugement immédiat dûment expliqué peut servir de base à une démonstration; celle-ci apparaît ainsi comme la mise en oeuvre des deux grands procédés généraux de notre pensée: l'intuition et le discours ou procédé discursif.
1) L'intuition en général est la connaissance d'un objet sans intermédiaire; elle est le propre des sensations et spécialement de la vision dont elle tire son nom et elle est l'idéal de l'intelligence. Mais elle revêt diverses formes, de valeur inégale. Il y a d'abord l'intuition vulgairement dite, puis l'intuition proprement dite.
a) L'intuition vulgairement dite (ou dans le langage courant) désigne toute connaissance directe d'un objet pris globalement, surtout dans le concret. On la trouve en particulier dans la perception sensible [§472]; dans la connaissance par connaturalité qui relève des lois de la vie affective [§717 et §794]; dans l'intuition divinatrice qui caractérise l'invention [§499]; ou au terme de la science dans la vue synthétique qu'on peut en obtenir [§600]. Mais ces procédés sont trop complexes et trop peu élaborés pour constituer des moyens aptes à conduire à la science; ils sont seulement diverses manifestations de notre vie consciente étudiées en psychologie.
b) L'intuition proprement dite est l'activité d'une fonction de connaissance par rapport à son objet propre. Elle peut être sensible ou intellectuelle; et c'est, comme nous venons de le dire, l'intuition intellectuelle, soit des premiers principes, soit des faits d'expérience qui constitue le point de départ de la démonstration. La psychologie en précisera les manifestations [°150], en distinguant l'intuition au sens large (vision immédiate, mais d'une vérité abstraite) et au sens strict (vision immédiate d'un objet réel existant); et la critériologie en démontrera la valeur d'infaillible vérité [§899].
2) Le discours ou procédé discursif est en général le passage d'une pensée à une autre; il prend de multiples formes, analysées en psychologie [°151] et nous avons signalé plus haut [§39] les trois formes du discours: la proposition, l'argumentation et le discours à intention pratique. Mais le procédé discursif qui conduit à la science est précisément le raisonnement sous sa forme parfaite qui est la démonstration.
Les jugements immédiats, base de la démonstration sont de deux sortes, comme nous l'avons dit [§15]: les jugements analytiques, dont l'évidence vient de l'analyse intellectuelle du sujet et du prédicat; et les jugements synthétiques qui relèvent de l'expérience sensible. Cette classification fait allusion à deux autres procédés généraux de la pensée: l'analyse et la synthèse qu'il convient de caractériser ici en notant leur rôle dans la démonstration.
§90) Analyse et synthèse. L'analyse est le procédé par lequel on passe d'un tout complexe aux éléments qui le composent ou aux principes qu'il implique.
La synthèse est le procédé par lequel on reconstruit l'unité d'un tout à partir de ses éléments; et, en général, c'est pour l'esprit la saisie d'un tout pris comme tel.
Ces procédés (ou manières d'agir) très généraux supposent toujours l'intervention de l'intelligence; cependant ils se rencontrent aussi en dehors de l'esprit et l'on doit d'abord distinguer l'analyse et la synthèse, soit réelles, soit idéales. Celles-ci (idéales) sont les actes mêmes de la pensée; celles-là (réelles) consistent dans la manipulation des choses de la nature; ainsi le chimiste par l'électrolyse fait l'analyse réelle de l'eau; et il peut ensuite la recomposer par une synthèse réelle [°152]. Il est clair d'ailleurs que ces manipulations s'effectuent sous la direction d'analyses ou de synthèses idéales dont elles ne sont que l'application ou la vérification. En logique, il suffit donc de considérer l'analyse ou la synthèse idéale.
Celles-ci se subdivisent en expérimentales et rationnelles. Elles sont rationnelles si elles portent sur des matières abstraites; expérimentales, si elles portent sur des objets ou faits concrets connus par l'expérience sensible et les jugements individuels unis dans la perception [°153]. Ce sont ces dernières qui dirigent les manipulations réelles, et les deux procédés, (expérimental et réel) tendent à se rejoindre, sans toujours y réussir; ainsi l'analyse de Condillac, isolant chacune de nos sensations, bien que expérimentale, restait purement idéale. La méthodologie des sciences positives en indique les règles, tandis que l'analyse et la synthèse rationnelles trouvent les leurs dans la logique exposée jusqu'ici.
L'analyse idéale est souvent une espèce de division [§36], à savoir une division essentielle qui expose les éléments constitutifs du tout, de façon à le rendre intelligible; ainsi, pour une machine, n'importe quelle séparation de partie est une division: mais l'analyse (ou la division analytique) sera la décomposition des diverses pièces suivant leur importance et leur rôle dans le mécanisme total.
Cependant, le terme «analyse» comporte aussi le sens de régression vers un élément simple et explicateur, même sans division; ainsi l'effort d'induction est analytique, parce qu'il résume dans une définition ou une loi simple un grand nombre de faits complexes, bien qu'il n'y ait pas proprement division. De même certaines démonstrations d'ordre idéal, comme la réduction à l'absurde et certaines preuves mathématiques sont analytiques, parce qu'elles ramènent la conclusion plus complexe aux principes plus simples; mais ce ne sont pas non plus des divisions.
D'où la définition générale de l'analyse: «procédé par lequel on passe d'un tout complexe aux éléments qui le composent ou aux principes qu'il implique»; et l'on peut distinguer l'analyse par division, «passage d'un tout à ses parties élémentaires plus simples»; et l'analyse par raisonnement: «passage par l'esprit d'un objet plus complexe à ses principes explicateurs ou ses raisons d'être plus simples».
§91). La synthèse rationnelle caractérise en particulier le jugement (affirmatif) où l'esprit, comme nous l'avons dit [§14 et §18] constate l'union dans une même nature du contenu représentatif de deux concepts; par exemple, ce qui est homme et ce qui est libre sont synthétisés dans le jugement «Tout homme est libre»; et l'on pourrait dire en un sens que tout jugement proprement dit (avec attribution formelle) est synthétique.
On distingue en effet parmi les formules courantes de jugements, l'attribution formelle et l'attribution par identité (ou matérielle); la première est celle où le prédicat exprime une nature qui est selon sa définition (formellement) différente du sujet; par exemple, l'homme est savant; l'homme est libre. La seconde est celle où l'attribut n'est que la définition partielle ou totale du sujet; par exemple, l'homme est raisonnable. Ce dernier jugement peut être appelé analytique au sens strict [°154], puisque l'identité affirmée du prédicat au sujet résulte uniquement et directement de l'analyse de ce dernier. Mais il n'est un jugement qu'au sens impropre; car il n'est encore qu'un simple concept explicité sous forme de jugement. Seule l'attribution formelle constitue un vrai jugement et elle réalise toujours en un sens une vraie synthèse, puisqu'elle enrichit le sujet d'un prédicat qui est extérieur à sa définition.
Mais l'analyse rationnelle peut aussi porter sur le prédicat; et elle pourra y découvrir un lien nécessaire avec le sujet, ou immédiatement, comme dans les propositions connues de soi: «Le tout est plus grand que sa partie»; ou médiatement, au moyen du syllogisme démonstratif; et il faut dire en ce sens que, soit les principes, soit les conclusions scientifiques, c'est-à-dire tous les jugements en matière nécessaire sont analytiques [°155]. Grâce en effet à ce lien nécessaire fondé sur la nature des choses, le prédicat, sans être une note de la définition du sujet (sans appartenir à sa compréhension logique), appartient cependant à sa compréhension réelle ou ontologique.
Quant au jugement d'expérience, comme: «Cette eau bout à 100 degrés Celcius», il est synthétique de toute façon; car il comporte une attribution formelle et l'analyse du prédicat n'y fait pas découvrir nécessairement le sujet; leur union est affirmée grâce à l'expérience qui est essentiellement contingente.
§92) Rôle de l'analyse et de la synthèse. L'analyse est surtout le procédé de l'invention et de la recherche; car les premières démarches de la pensée ne nous livrent l'objet d'étude qu'en gros, comme un tout complexe et confus; c'est une synthèse, si l'on veut, mais implicite et vague [°156]. Il faut donc diviser l'objet pour retrouver les éléments explicateurs, préciser les points de vue par abstraction, remonter aux définitions et aux principes par induction; démarches éminemment analytiques.
La synthèse de son côté construit les sciences parfaites [§17]; elle montre, degré par degré, les raisons d'être pleinement explicatives de toutes les propriétés connaissables d'un objet donné; elle permet ainsi les définitions essentielles et les concepts complets; la géométrie avec son enchaînement de théorèmes en est un bon exemple. C'est pourquoi aussi elle est le procédé par excellence de l'enseignement, conduisant l'esprit en pleine lumière vers les conclusions vraies.
Toute science, peut-on dire, commence par un mouvement d'analyse appelé induction; a pour centre une définition, et s'achève par un mouvement de synthèse appelé déduction.
Il y a pourtant des sciences en formation où l'induction analytique reste le procédé dominant, tandis que des synthèses partielles y suggèrent souvent des hypothèses fécondes pour de nouveaux progrès; de la sorte, la synthèse devient un instrument de découverte et l'analyse, un moyen d'enseignement. D'ailleurs, même dans les sciences parfaites, il est bon parfois de se mettre en présence des procédés d'invention en refaisant quelques analyses.
Bref, ces deux procédés très généraux de notre esprit se rencontrent à chaque pas dans nos sciences qui ne sont, a-t-on dit justement, «qu'une analyse entre deux synthèses». Mais ils sont trop complexes et trop vagues pour remplacer, quoiqu'en ait dit Descartes [°157], toutes les autres règles de la logique.
§93) Notion et division. Dans les sciences en formation et dans les discours où il s'agit de persuader plus que de démontrer, on rencontre des raisonnements impeccables au point de vue de la logique formelle, mais qui ne donnent pas pleine évidence; ils restent donc dans la vraisemblance. Les anciens les appelaient dialectiques [°158] parce qu'on peut en discuter, tandis que la démonstration est qualifiée d'apodictique [°159] (manifeste). Ils ne sont pas cependant inutiles, parce qu'ils s'approchent de la vérité en fondant des opinions probables qu'il convient d'accepter, faute de mieux.
On appelle opinion probable, une affirmation où l'esprit adhère positivement à l'une des deux contradictoires, mais en gardant quelque crainte d'erreur, ce qui exclut la certitude et la science [§585 et §595].
Le domaine par excellence de la probabilité est celui des faits contingents, spécialement des événements futurs dépendant du hasard [°160] ou de la liberté humaine. Les mathématiques ont ici précisé la notion en y considérant l'aspect de nombre. On appelle alors probabilité d'un événement, le rapport entre le nombre des cas favorables et le nombre des cas possibles; par exemple, si un sac contient 100 boules dont une blanche, il y a une chance sur 100 qu'en puisant au hasard, on rencontrera la boule blanche. On peut calculer ce rapport de probabilité soit a priori, d'une façon rigoureuse, quand le nombre des cas possibles et celui des cas favorables sont bien déterminés d'avance, comme dans l'exemple donné; soit a posteriori, en observant un grand nombre de cas, où la méthode des statistiques permet d'établir une moyenne; on déterminera par exemple, selon quel pourcentage la probabilité de vivre encore 10 ans est plus grande à 40 ans qu'à 60 ans. Le calcul de ces probabilités est une section des sciences mathématiques.
Mais lorsqu'il s'agit d'approcher une vérité spéculative, comme une loi ou une définition; et dans les cas de prévision dépendant de facteurs qualitatifs (réussite à un examen, par exemple), ce calcul rigoureux n'est plus possible. La probabilité mathématique est remplacée par une probabilité psychologique fondée sur l'appréciation des motifs d'évidence. Ainsi, dans les sciences, en particulier les sciences positives, les premières inductions, surtout sous la forme imparfaite de l'argument par analogie, n'aboutissent d'abord qu'à des probabilités. Quant aux syllogismes, ils restent dialectiques ou probables, chaque fois que l'une des prémisses, (ordinairement la majeure) est une affirmation seulement probable, comme sont les opinions courantes, les sentences proverbiales, etc. Les principes probables sont nombreux; Aristote les a groupés sous quatre chefs ou lieux (en grec τόπος) d'où le titre de topiques donné à cette partie de la logique. Ces quatre lieux sont le genre, la définition, le propre et l'accident [°161].
C'est l'application vigilante et impartiale des règles d'une saine, critique, uniquement inspirée par l'amour du vrai qui permet de distinguer la démonstration scientifique, du simple raisonnement dialectique, qui n'aboutit encore qu'à une opinion probable.
§94) Notion et division. Le sophisme [°162] est un raisonnement qui, sous les apparences de la rectitude, cache un défaut en raison duquel il conclut à l'erreur. On l'appelle aussi paralogisme lorsqu'il pèche à l'insu du penseur qui l'emploie. On en distingue deux grandes classes: Le sophisme de forme qui pèche contre une des lois de la logique formelle; le sophisme de matière, qui, en observant ces lois, aboutit à l'erreur en raison des choses dites. Les uns et les autres concernent les deux formes de raisonnement.
1) Dans le syllogisme, on cite a) comme principaux sophismes de forme:
1.1) L'équivoque verbale, où un même terme est pris en deux sens différents; par exemple:
Tout chien est vivant, Or, une partie du fusil est un chien, Donc une partie du fusil est vivante.
Ce syllogisme pèche contre la règle des trois termes: il y en a en réalité quatre.
1.2) Le passage d'un sens à un autre, du sens divisé au sens composé ou du sens propre au sens figuré; par exemple:
Celui qui est assis ne peut marcher, Or vous êtes assis, Donc vous ne pouvez marcher.
Ou encore:
Celui qui fait des châteaux dans un pays doit y payer l'impôt, Or Jean fait des châteaux en Espagne, Donc Jean doit payer l'impôt en Espagne.
Ces sophismes sont des variétés de l'équivoque.
1.3) L'amphibologie par laquelle une proposition mal construite peut avoir deux sens; par exemple:
2 fois 3 et 2 = 8, Or, 10 = 2 fois 3 et 2, Donc 10 = 8.
Le latin en fournit d'autres exemples avec les propositions infinitives, comme, «Aio te Romanos vincere posse» [°163].
b) Comme sophismes de matière signalons:
1.4) L'accidentel considéré comme essentiel, ou vice-versa; par exemple:
Tout ce qui exerce une mauvaise influence est essentiellement mauvais, Or l'état social exerce une mauvaise influence, Donc l'état social est essentiellement mauvais (Jean-J. Rousseau).
1.5) L'ignorance de la question (ignorantia elenchi), lorsque la chose démontrée n'est pas celle qu'on demande; par exemple, pour faire acquitter un voleur, l'avocat démontre qu'il est un vaillant soldat.
1.6) La pétition de principe où l'une des prémisses est précisément la conclusion à établir; par exemple, pour prouver que Pierre est fils de Zébédée, on part de ce fait que Zébédée est père de Pierre.
1.7) Le cercle vicieux est une double pétition de principes où, après avoir prouvé une première affirmation par une seconde, on prouve la seconde par la première; ainsi Descartes prouvait l'existence de Dieu par l'idée claire; et fondait la valeur de l'idée claire sur l'existence de Dieu.
2) En induction, le sophisme a principalement trois sources:
2.1) Une mauvaise observation; le désir de trouver une preuve, par exemple, fait qu'on croit voir des circonstances ou même des faits qui n'existent pas en réalité.
2.2) Une interprétation inexacte (sophisme «post hoc, ergo propter hoc») où l'on prend une coïncidence fortuite pour la cause; parce qu'un malheur est arrivé le jour où l'on était 13, le nombre 13 porte malheur.
2.3) Une énumération insuffisante, (sophisme «ab uno disce omnes»); parce qu'on a été volé par un habitant de Liège, on conclut: «Les liégeois sont voleurs».
Le seul moyen efficace pour éviter tous les paralogismes et réfuter tous les sophismes, est la connaissance approfondie du sujet, acquise par un effort patient et persévérant. Mais la connaissance des règles de la logique est déjà une garantie, soit pour dépister les sophismes de forme, soit pour mener à bien, plus sûrement et plus aisément, le labeur de la science.
[précédente] [suivante]
Adorons Jésus-Eucharistie! | Accueil >> Varia >> Livres >> Précis de philosophie